Quinze pavages pentagonaux, et pas un de plus !
En géométrie, certaines questions apparemment simples peuvent mettre les scientifiques en difficulté durant des décennies, voire des siècles. Or, en s’aidant d’un programme informatique, un chercheur français vient de résoudre une énigme lancée il y a près de cent ans.
Olivier Boulanger - Publié le
C’est un problème aussi vieux que la géométrie : comment recouvrir une surface d’un motif unique répété à l’infini ? Dès l’Antiquité, cette question s’est posée afin de produire des mosaïques ou des carrelages aux qualités esthétiques. Si l’on s’intéresse aux polygones réguliers, ce n’est pas trop compliqué : seuls les triangles, les carrés et les hexagones conviennent.

Pour les polygones irréguliers convexes, c’est un peu plus restrictif : ça marche pour tous les triangles, pour tous les quadrilatères, mais seulement pour trois types d’hexagones.
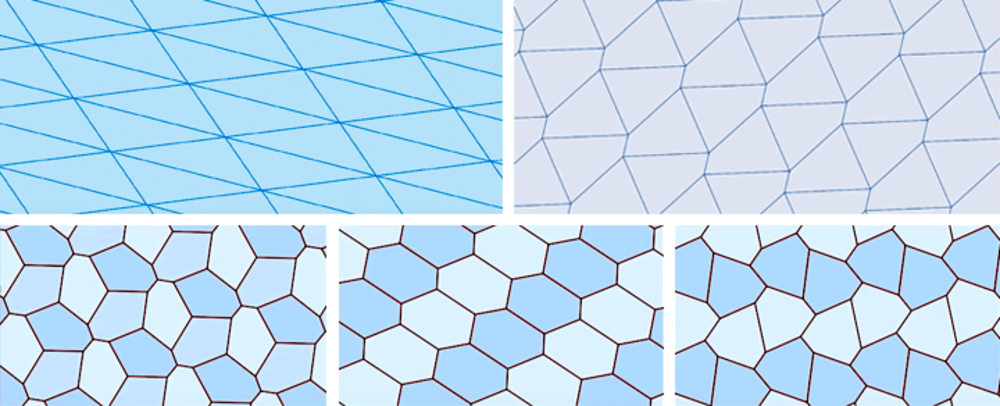
Pour les pentagones en revanche – c’est-à-dire les polygones à cinq côtés – la question est plus délicate. En 1918, le jeune Karl Reinhardt a pu démontrer dans sa thèse que cinq types de pentagones – pas un de plus ! – pouvaient se comporter comme des pavés.
Inventaire
Bien vu... mais depuis la fin des années 1960, d’autres formes ont pu être découvertes, par des chercheurs très souvent, mais aussi par des mathématiciens amateurs comme Marjorie Rice qui en découvrit quatre au cours des années 1970. Dernier en date, celui mis en évidence il y a deux ans par une équipe de l’université de Washington, portant ainsi à quinze le nombre de pentagones pouvant être utilisés au sein d’un pavage.

Mais une question restait en suspens. Pouvait-il en exister d’autres ? La réponse vient de tomber grâce à la sagacité du Français Michaël Rao, de l’université Claude Bernard de Lyon. À grand renfort d’informatique, le chercheur a pu générer tous les pavages pentagonaux possibles et confirmer, qu’effectivement, seuls 15 d’entre eux pouvaient satisfaire les conditions requises.
Extrait du programme conçu par Michaël Rao
Grâce à cette approche, Michaël Rao clôt donc un problème vieux d’un siècle. Et la même méthodologie pourrait maintenant être mise à profit pour résoudre d’autres énigmes concernant les pavages, et notamment ceux dits « non convexes », c’est-à-dire possédant des angles rentrants.

