Entre silence et soupirs

Andreatta Moreno, à l'Ircam Mathématicien et musicien, ce chercheur travaille sur les représentations géométriques de la musique. © CSI 2008

Les deux pieds empêtrés dans un enchevêtrement de fils électriques noirs ou gris, Andreatta Moreno, chercheur à l'Ircam*, palpe l'arrière du clavier qui gît dans un recoin de son bureau. À cause du manque de lumière, il écarquille les yeux ; à cause du manque de solution, il se gratte la tête avec la régularité d'un métronome. « Je ne comprends pas… pourquoi ça marche pas… », répète-t-il avec son accent italien. Après un court silence, il se redresse, replace ses petites lunettes et sourit, un brin embêté. « Je vais aller chercher du renfort, je crois… » Il faut croire que l'on ne peut pas être à la fois musicien, théoricien, mathématicien et… technicien. Il réapparaît quelques minutes plus tard, désigne le clavier à un jeune homme et explique : « Ça ne marche pas ». Sur quoi, il s'installe sur une chaise moelleuse tandis que son confrère commence à démêler une pelote de fils. « Alors comme ça, Dmitri Tymoczko a encore fait des siennes ? » sourit-il.

Le modèle de Dmitri Tymoczko Sur ce graphique, chaque point représente une association de trois notes, autrement dit un accord. Dans ce modèle, publié récemment dans « Science », presque tous les points peuvent bouger dans six directions différentes. Pour en savoir plus, regardez la vidéo portant sur les représentations. Ce schéma n'est qu'une extension du dernier mode de représentation présenté dans le film. © Science

Dmitri Tymoczko, chercheur à l'université américaine de Princeton, est, à l'instar d'Andreatta Moreno, théoricien de la musique. Tous deux travaillent sur les modes de représentation géométrique de la musique qui portent sur la mélodie, le rythme, l'intensité, le timbre ou l'harmonie (l'analyse des accords). Et justement, d'après un article paru dans Science le 17 avril 2008, Dmitri Tymoczko et son équipe seraient parvenus à généraliser les représentations géométriques de l'harmonie. « Qu'est-ce que cela signifie ?! Vous allez voir, c'est simple… » Il pivote sur la chaise. « Toujours rien du côté du clavier ? » « Nan… » grommelle le jeune homme. « Tant pis, je vais faire sans. » Il fait à nouveau volte-face.

* Institut de Recherche et Coordination Acoustique/Musique

Musique et géométrie, des sœurs qui s'ignorent ?

© CSI 2008

« En fait, il existe beaucoup de similitudes entre la géométrie et la musique. Si l'on prend un accord simple, par exemple un mélange de trois notes comme do, mi et sol. » Le voilà qui frappe les notes dans le vide. « Vous pouvez les jouer ensemble. » Sa main fouette l'air puis revient en place. « Translater l'accord, c'est-à-dire le déplacer dans la gamme en gardant l'espacement entre les notes ». Sa main fait maintenant des petits bonds de gauche à droite. « Ou encore inverser l'accord ». Ses doigts s'agitent dans un sens, dans l'autre, puis s'affalent sur son genou. « Evidemment… ce serait mieux avec le son », sourit-il. « Bref, l'idée est de trouver des représentations visuelles, géométriques, qui pourraient rendre compte, révéler, les relations entre chaque accord. »

Dans la musique occidentale, on estime qu'il existe cinq types de transformations d'accords qui peuvent être décrites de façon géométrique : le déplacement à l'octave, la permutation, la transposition, l'inversion et le changement de cardinalité. Pour les théoriciens de la musique, l'idée est donc de trouver des représentations visuelles, géométriques permettant de révéler des relations entre les accords, « d'établir les nerfs topologiques, c'est-à-dire de savoir quelles transformations permettent de passer d'un accord majeur à un accord mineur, d'un septième à un diminué, etc… »

Prenez un cours de géométrie musicale !

Jeux de notes, jeux de polygones

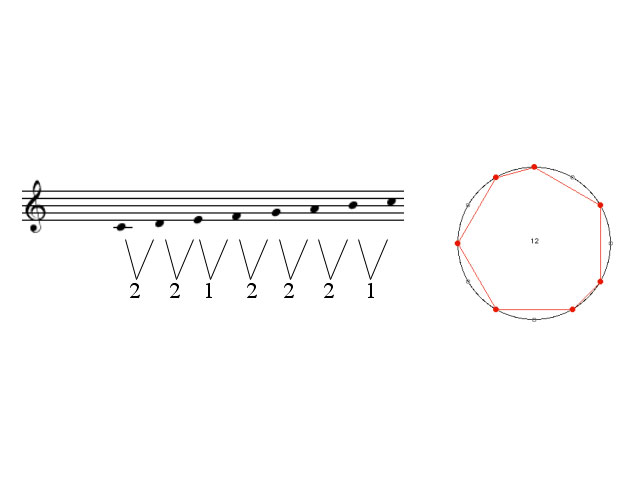
Les notes de la gamme placées sur une représentation en cercle Pour obtenir une représentation circulaire, il suffit de placer tous les demi-tons sur un cercle est de joindre (ici, par un trait rouge) les notes jouées. © CSI 2008

Pour ce faire, historiquement, les chercheurs ont commencé par utiliser des représentations circulaires. La gamme diatonique (do ré mi fa sol la si) étant composée de 12 demi-tons (do do# ré ré# mi fa fa# sol sol# la la# si), il est possible de disposer les demi-tons sur un cercle, comme on le ferait avec les heures d'une horloge. Par la suite, en reliant tous les demi-tons joués, on dessine, pour chaque accord, un polygone. On peut alors observer les transformations géométriques qu'il est nécessaire d'appliquer pour passer d'un accord à un autre. Via la représentation du cercle, on observe ainsi des transpositions… mais pas le décalage à l'octave par exemple. D'où l'intérêt de la représentation spatiale de Dmitri Tymoczko qui, pour la première fois, explicite toutes les transformations géométriques nécessaires pour passer d'un accord à un autre.

« En fait, cette représentation est une extension d'un travail qu'il a publié en 2006. A l'époque, il n'était parvenu à inclure que quelques accords dans son modèle. Aujourd'hui, tous les accords connus dans la gamme diatonique y figurent ». Andreatta Moreno lorgne quelques instants le modèle de Tymoczko. « Mais attention, contrairement à ce que ce graphique laisserait croire, ce modèle s'inscrit non pas dans trois dimensions, mais dans quatre ! ». Il se redresse. « En fait, d'un point de vue géométrique, les notes n'évoluent pas dans un plan, elles forment des singularités mathématiques, des dessins inconnus de la géométrie euclidienne ! » Sa gestuelle gagne en amplitude. « La musique partage avec les mathématiques une beauté formelle unique et… ». « Ça y est ! » lâche le jeune homme au piano. Un temps surpris par l'intervention, Andreatta Moreno reprend son mouvement et lève les mains au ciel. « Bravo ! Merci ! ». En un clin d'œil, le chercheur se retrouve au piano pour des explications que nous vous proposons de suivre en vidéo.

À quoi servent ces recherches ?

Andreatta Moreno manque de s'étrangler. « Comment ça, à quoi servent ces recherches ? » Il brandit à nouveau les mains vers le ciel. « Mais à pleins de choses ! », s'enthousiasme-t-il.

« Quand on apprend la musique dans une école par exemple, on néglige les principes théoriques qui ont un caractère formel… une validité qui dépasse le cadre du style. Par exemple, quand on fait de l'harmonisation, on explore des techniques sans se rendre compte que, derrière elles, il y a des structures algébriques cachées qui peuvent être appliquées à d'autres types de situation musicale ! » Il garde le silence quelques secondes.

« Et puis aujourd'hui, en Occident, on n'écrit plus de la musique comme on le faisait au XIXe siècle. Les compositeurs peuvent choisir de travailler sur une gamme non plus divisée en 12 tons, mais en 72 ! Il est alors nécessaire d'utiliser les mathématiques pour dresser la liste des accords possibles dans ce nouveau référentiel… » Il sourit. « Et aider les compositeurs à créer de nouveaux types de désordres organisés… »

Liens externes