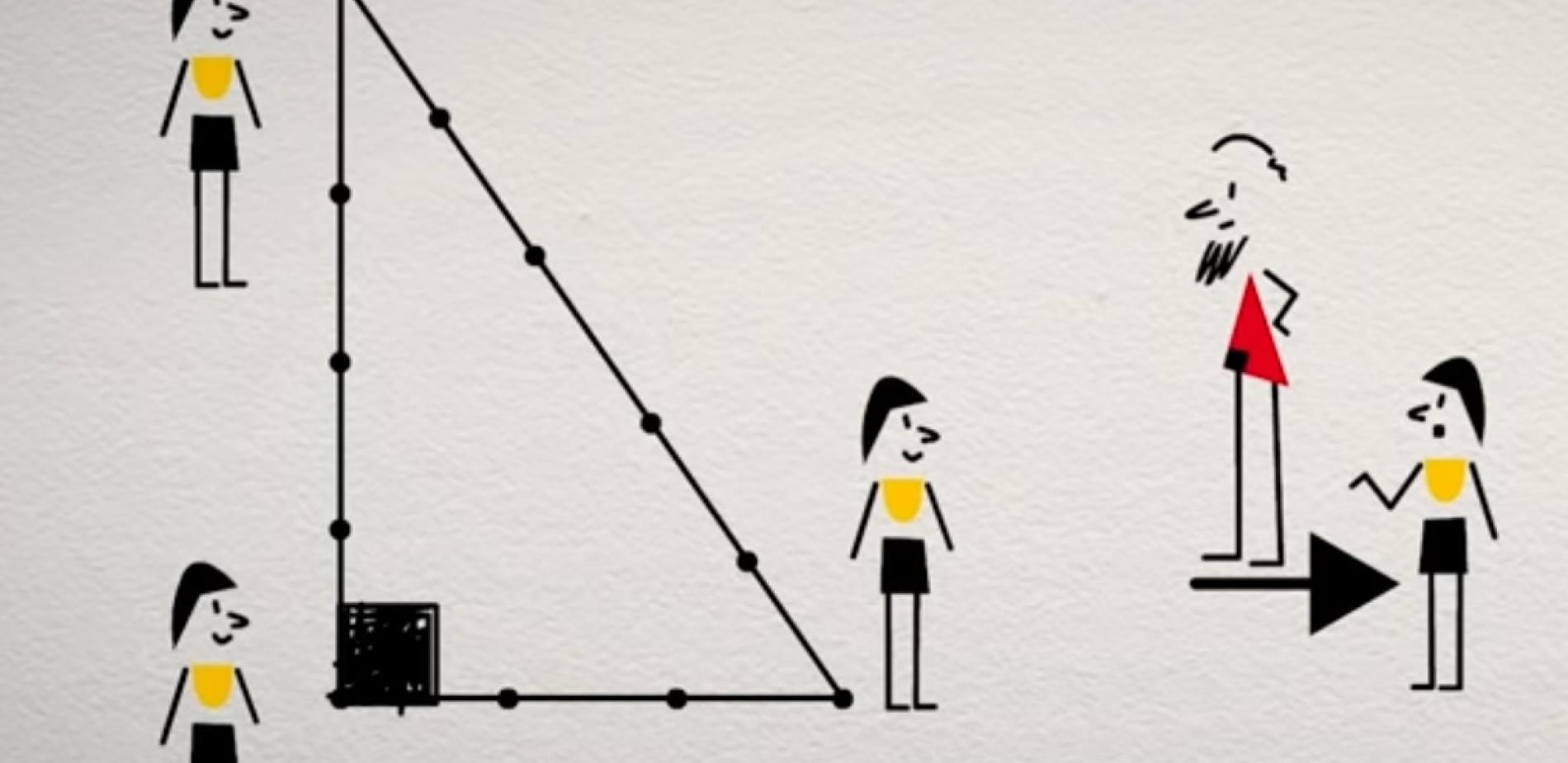
Le théorème de Pythagore Disons le tout net, sans le théorème de Pythagore, il n’y aurait pas de philosophe, pas la réciproque du théorème, pas de triangles rectangles en B, et donc par extension, pas d’angles droits, donc pas de maison qui se tiendrait bien droite "au carré", pas de salle de bains, pas de cuisine, pas de chambre, tout serait de travers… et bien d’autres choses encore. Pythagore est né à Samos, une île grecque, au 6e siècle avant Jésus-Christ. On connaît bien son théorème mais on connaît mal Pythagore. C’était un homme très discret. On sait tout de même qu'il a beaucoup voyagé. Pas très loin d’abord, à Milet. Là, il rencontre Thalès. Thalès et Pythagore sont les fondateurs des mathématiques grecques. Ils ont du avoir beaucoup de choses à se dire. Mais ils n’ont rien écrit, alors on n’est pas bien sûr. On sait ensuite que Pythagore est allé s’installer en Egypte. Et là… Il tombe sur une drôle de corde avec des nœuds, très exactement 13 nœuds. Les architectes égyptiens s’en servent pour construire de belles pyramides avec de beaux angles droits. - Comment faites-vous donc ça ? demande Pythagore - Cette corde c’est comme une équerre, qu’il lui disent. On tend la corde en trois points : n° 4, 8 et 13… on tend bien comme ça là et hop !!! l’angle il est bien droit - Et comment expliquez vous cela, demande Pythagore ? - Nous, on n’explique pas, répondent les architectes. L’esprit mathématique de Pythagore fait un tour sur lui-même. L'évidence est une curiosité que je ne saurais admettre... J'aimerais comprendre... Je dois comprendre. Je dois piger cette chose qui fait que 3,4,5 et hop un angle droit ! Quel drôle de phénomène... 3+4=7-5=2 non je ne vois pas… Tiens ? Maman... Elle est toute de travers ! Et si j’essaye avec des carrés… 3, 4… 3, 9, 4, 16… Ca s’additionne !!! Voilà !! Le théorème de Pythagore est né. Et il formule la chose ainsi : Dans un triangle rectangle, le carré du grand côté est égal à la somme des carrés des petits côtés. a2 + b2 = c2 Et ce n'est pas tout : Pythagore l’explique et maintenant qu'il a compris, il démontre ! Avec son théorème et sa démonstration, il part révéler l'incroyable vérité. Parce que démontrer, c'est aussi partager. Et celui qui n’est pas d’accord ? Il n’a qu’à le dire ! On en discute.