Un amateur découvre une forme mathématique inédite et épate les plus grands savants
Publié le - par Le Blob, avec l’AFP

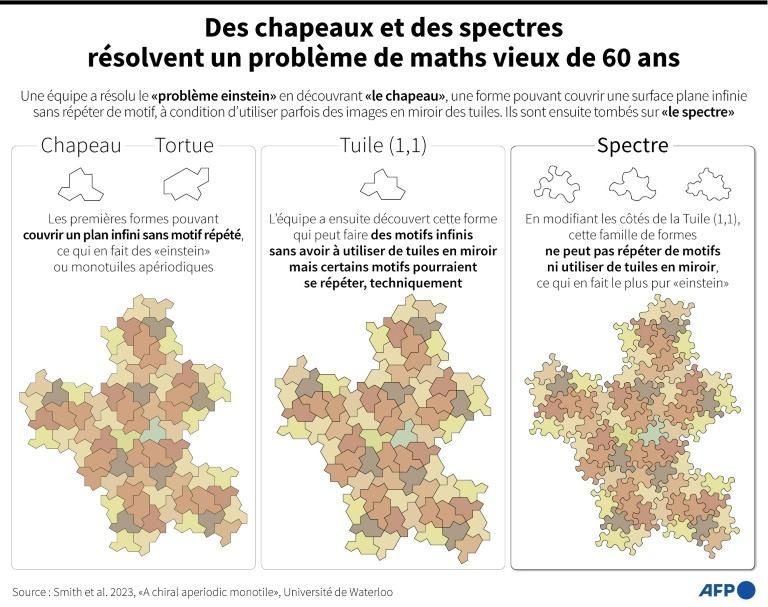
Chercher un motif géométrique « étonnant » : tel est le passe-temps favori de David Smith, paisible retraité britannique. En novembre, il est tombé sur une forme inédite aux propriétés remarquables, déchaînant l’enthousiasme d’une communauté de passionnés. Et l’admiration des savants. Après qu’il a rendu publique sa découverte en mars dernier, ces amateurs d’un genre particulier ont imprimé sur des t-shirts cette nouvelle forme, confectionné des biscuits selon ce motif et même envisagé de se la tatouer sur le corps. Ce polygone à treize côtés, baptisé « le chapeau », est le premier motif qu’on puisse assembler à l’infini sans faire apparaître un motif d’ensemble qui se répète — par exemple, un losange assemblé à l’infini à d’autres losanges produira à un moment donné un grand losange.
À ce titre, « le chapeau » est le premier « einstein », du nom d’un problème posé il y a 60 ans et que les mathématiciens supposaient insoluble. David Smith, 64 ans, a fait mieux depuis, avec « le spectre ». Car « le chapeau » avait un petit inconvénient : il fallait retourner le motif une fois tous les sept coups (ou toutes les sept pièces, comme pour un puzzle) pour éviter l’apparition d’une même forme se répétant. Le retraité, avec l’aide de trois mathématiciens, a démontré, dans une étude à paraître, que « le spectre » est un pur « einstein ». Ce dernier nom est tiré de l’allemand « ein Stein » (une pierre), et sans rapport avec celui du célèbre physicien.
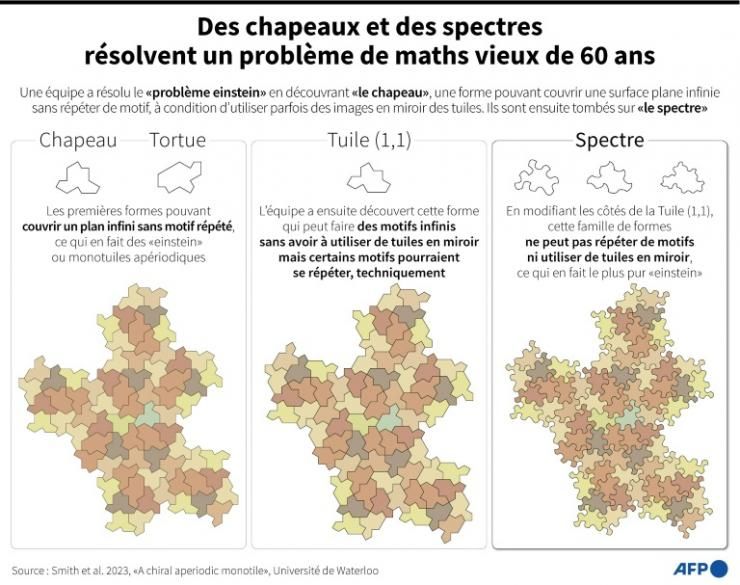
Chapeau, tortue et spectre
Pour Craig Kaplan, professeur d’informatique à l’Université canadienne de Waterloo, c’est « une histoire amusante et presque ridicule, mais merveilleuse ». Il raconte avoir été contacté en novembre 2022 par M. Smith, ancien technicien d’imprimerie dans le Yorkshire (nord de l’Angleterre) : il avait trouvé un motif « qui ne se comportait pas de la façon dont on pouvait s’y attendre ». Si on assemblait plusieurs exemplaires de ce motif sur une table, aucun motif d’ensemble n’y apparaissait. Un programme informatique a confirmé qu’il s’agissait du premier « einstein », appelé également en langage savant une « mono-tuile apériodique ». Leur travail a été remarqué par un adepte du maniement de ces tuiles, le chercheur japonais Yoshiaki Araki, qui a créé des œuvres d’art à l’aide du « chapeau » et d’une variante appelée « la tortue ».
Encouragé, notre retraité britannique tente alors de trouver un nouveau motif ne nécessitant pas de le retourner périodiquement. Mission accomplie en moins d’une semaine, face à un Craig Kaplan incrédule. Mais une analyse a bien confirmé que cette nouvelle tuile était « un einstein sans inversion », ajoute l’informaticien canadien. Et pour s’en assurer définitivement, l’amateur et le scientifique ont même « amélioré » la forme, de façon à ce qu’elle ne puisse pas être utilisée avec une inversion. « Le spectre » était né.
« Tombée du ciel »
Les deux articles scientifiques sont encore à l’étude dans des revues scientifiques avant publication, mais le monde des mathématiques n’a pas attendu pour commenter la nouvelle. Cette découverte est « excitante, surprenante et étonnante », déclare Marjorie Senechal, mathématicienne au Smith College (Massachusetts). Qui y voit plus qu’une simple belle histoire. Le nouveau motif et ses variantes devraient « mener à une compréhension plus profonde de l’ordre dans la nature et de la nature de l’ordre ».
Pour Doris Schattschneider, mathématicienne à la Moravian University (Pennsylvanie), les deux formes sont « impressionnantes ». Même le mathématicien et Nobel de physique 2020 Roger Penrose, spécialiste des tuiles apériodiques, doutait qu’un tel exploit soit possible, relève-t-elle. La prestigieuse Université d’Oxford organise en juillet un événement célébrant cette découverte, le Hatfest (fête du chapeau), auquel participera Roger Penrose. Cette découverte est d’autant plus étonnante que « la réponse est tombée du ciel et des mains d’un amateur », souligne Craig Kaplan. « Et de la plus belle façon, grâce à un amoureux du sujet, qui l’explore en dehors de tout objectif professionnel ».